What tidal diamonds mean and how they are used
A tidal diamond is a way of describing the average tidal current conditions for a location by referencing them to the time of high water (either at the same location or at a remote location or port). Each diamond gives the average current speed and direction over a complete tidal cycle from six hours before the time of high water to six hours after. Usually two sets of values are given – one for spring tides and another for neap tides.
Traditionally, these values are derived from a very short period (13 or 25 hours) of observations during a meteorologically quiet period from a current meter deployed just below the sea surface from an anchored vessel. The name ‘diamond’ is derived from the symbol used on Admiralty charts to indicate the location of these observations.
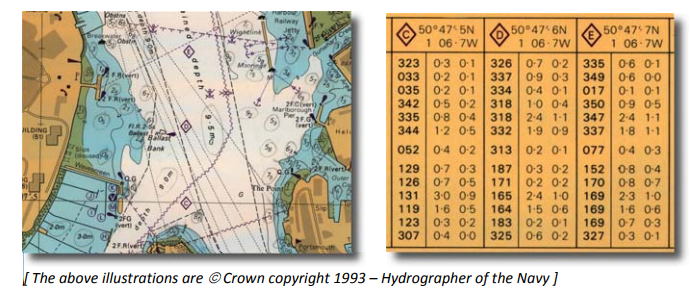
Each diamond on an admiralty chart consists of three columns of numbers. The first gives the direction of current flow clockwise from true north, the second is the speed in knots during spring tide, the third is the speed during neap tide. The thirteen rows represent the time from six hours before high water to six hours after. The reference location is usually a nearby port – in the example above, this is Portsmouth.
Example
If you require the current speed at 2:30pm at diamond D, you first find the nearest high water at Portsmouth. Say this was at 10:30am, then 2:30pm is four hours after high water. Therefore the currents at diamond D at 2:30pm will be about 1.5 knots during springs or 0.6 knots at neaps and flowing S‐SE (164°). An hour later, the current will have almost completely died away.
Observation diamonds and modelled diamonds
There are many disadvantages to tidal diamonds derived in the traditional way:
Usually based on a very short period of observations (often less than 25
hours).
- Was the period of observation meteorologically quiet?
- Observations must be taken during an average spring and neap tide as there can be significant differences between successive springs and neaps.
- Expensive to generate, hence they can be very sparse and unevenly distributed as one gets further from a harbour. To increase the accuracy of a diamond by any significant amount would require a minimum of 30 days observations and this is just not feasible. Using computer models of the ocean to generate the diamonds solves all of these problems.
- A longer period of ‘virtual observations’ can be used to compute the diamond.
- A computer tidal model does not have any meteorological effects.
- Using all the springs and neaps throughout a period of a year produces a diamond for an average spring and neap.
- Once the model has been developed, diamonds can be computed for any location within the model domain.
- Computer models are based on a regular grid, hence computed diamonds can be evenly and regularly spaced.
